一、实验目的
1、了解香农编码的基本原理及其特点;
2、熟悉掌握香农编码的方法和步骤;
3、掌握Matlab编写香农编码的程序。
二、实验内容
1、写出香农编码的Matlab程序;
2、将程序在计算机上仿真实现,验证程序的正确性并完成仿真。
三、实验原理及说明
给定某个信源符号的概率分布如下,通过以下的步骤进行香农编码:
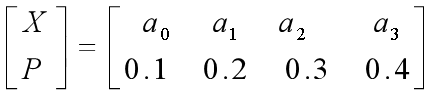
1、信源符号按概率从大到小排列。
2、对信源符号求累加概率,表达式:Gi=Gi-1+p(xi)。
3、求自信息量,确定码字长度。自信息量I(xi)=-log(p(xi));码字长度取大于等于自信息量的最小整数。
4、将累加概率用二进制表示,并取小数点后码字的长度的码。
四、实验设备
1、计算机
2、软件:Matlab
五、实验方法
实验仿真程序如下:
1.主程序
pa=input('请输入信源分布:')
k=length(pa); %计算信源符号个数
if min(pa)<0||max(pa)>1 %判断信源概率值是否介于0到1之间
disp('概率值必须介于0到1之间,请重新输入信源分布');
return
elseif sum(pa)~=1 %判断信源累加和是否为1
disp('概率累加和必须等于1,请重新输入信源分布');
return
else
for i=1:k-1 %for循环进行降序排列
for n=i+1:k
if (pa(i)<pa(n))
t=pa(i);
pa(i)=pa(n);
pa(n)=t;
end
end
end
end
disp('信源分布概率从大到小为:'),disp(pa)
y=0;%给y赋初值,用来求概率和
f=0;%给f赋初值,用来得到子程序最大循环次数
s=zeros(k,1); %对求和结果进行矩阵初始化
b=zeros(k,1); %对编码位数矩阵初始化
w=zeros(k,1); %对二进制矩阵初始化
for m=1:k; %进行香农编码
s(m)=y;
y=y+pa(m);
b(m)=ceil(-log2(pa(m)));%求得的自信息量向上取整,得到码字长度
z=zeros(b(m),1); %对码字矩阵初始化
x=s(m);
f=max(b(m)); %把码字最大长度赋给f,用于进行十进制转二进制
w=dtob(x,f); %调用子程序将十进制转换为二进制
for r=1:b(m)
z(r)=w(r);
end
disp('输出结果为:');
disp('初始概率'),disp(pa(m))
disp('求和结果'),disp(s(m))
disp('编码位数'),disp(b(m))
disp('最终编码'),disp(z')
end
sum0=0;
sum1=0;
for i=1:k %使用for循环进行信息熵、平均码长求解
a(i)=-log2(pa(i)); %a(i)表示单个信源的自信息量
K(i)=ceil(a(i)); %K(i)表示对自信息量向上取整
R(i)=pa(i)*K(i);
sum0=sum0+R(i); %求平均码长
c(i)=a(i)*pa(i);
sum1=sum1+c(i); %信息熵
end
K1=sum0;
H=sum1;
Y=H/K1; %用Y来表示编码效率
disp(['信息熵H(X)=',num2str(H),'(bit/sign)']);
disp(['平均码长K=',num2str(K1),'(bit/sign)']);
disp(['编码效率=',num2str(Y)]);
2.调用子程序:
function y=dtob(x,f)
for i=1:f
temp=x.*2;
if(temp<1)
y(i)=0;
x=temp;
else
x=temp-1;
y(i)=1;
end
end
仿真结果如下:
请输入信源分布:[0.1 0.2 0.3 0.4]
信源分布概率从大到小为:
0.4000 0.3000 0.2000 0.1000
输出结果为:
初始概率
0.4000
求和结果
0
编码位数
2
最终编码
0 0
输出结果为:
初始概率
0.3000
求和结果
0.4000
编码位数
2
最终编码
0 1
输出结果为:
初始概率
0.2000
求和结果
0.7000
编码位数
3
最终编码
1 0 1
输出结果为:
初始概率
0.1000
求和结果
0.9000
编码位数
4
最终编码
1 1 1 0
信息熵H(X)=1.8464(bit/sign)
平均码长K=2.4(bit/sign)
编码效率=0.76935