一、实验目的
1、了解Huffman编码的基本原理及其特点;
2、熟悉掌握Huffman编码的方法和步骤;
3、掌握Matlab编写Huffman编码的程序。
二、实验内容
1、写出Huffman编码的Matlab程序;
2、将程序在计算机上仿真实现,验证程序的正确性并完成仿真。
三、实验原理及说明
某个信源符号的概率分布如下:
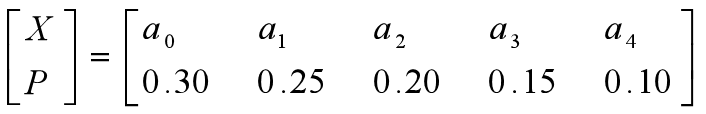
通过以下的步骤进行Huffman编码:
1、将q个信源符号按概率递减的方式排列。
2、用0、1码符号分别表示概率最小的两个信源符号,并将这两个概率最小的信源符号合并成一个新的符号,从而的得到的只含q-1个符号的新信源,称为信源的缩减信源。
3、将缩减信源中的符号仍按概率大小以递减次序排列,重复步骤(2)。
4、重复(1)(2)(3)三步骤,直至缩减信源只剩下两个符号为止,将这最后两个符号分别用0、1码字表示。
5、从最后一级缩减信源开始,向前返回,得出各信源符号所对应的码符号序列,即为对应信源符号的码字。
四、实验设备
1、计算机
2、软件:Matlab
五、实验方法
实验仿真代码如下:
p=input('please input a number:') % 提示输入界面
n=length(p);
for i=1:n
if p(i)<0
fprintf('\n The probabilities in huffman can not less than 0!\n');
p=input('please input a number:') % 如果输入的概率数组中有小于 0 的值,则重新输入概率数组
end
end
if abs(sum(p)-1)>0
fprintf('\n The sum of the probabilities in huffman can more than 1!\n');
p=input('please input a number:') % 如果输入的概率数组总和大于 1 ,则重新输入概率数组
end
q=p;
a=zeros(n-1,n); % 生成一个 n-1 行 n 列的数组
for i=1:n-1
[q,l]=sort(q) % 对概率数组 q 进行从小至大的排序,并且用 l 数组返回一个数组,该数组表示概率数组 q 排序前的顺序编号
a(i,:)=[l(1:n-i+1),zeros(1,i-1)] % 由数组 l 构建一个矩阵,该矩阵表明概率合并时的顺序,用于后面的编码
q=[q(1)+q(2),q(3:n),1]; % 将排序后的概率数组 q 的前两项,即概率最小的两个数加和,得到新的一组概率序列
end
for i=1:n-1
c(i,1:n*n)=blanks(n*n); % 生成一个 n-1 行 n 列,并且每个元素的的长度为 n 的空白数组, c 矩阵用于进行 huffman 编码,并且在编码中与 a 矩阵有一定的对应关系
end
c(n-1,n)='0'; % 由于 a 矩阵的第 n-1 行的前两个元素为进行 huffman 编码加和运算时所得的最
c(n-1,2*n)='1'; %后两个概率,因此其值为 0 或 1 ,在编码时设第 n-1 行的第一个空白字符为 0 ,第二个空白字符 1 。
for i=2:n-1
c(n-i,1:n-1)=c(n-i+1,n*(find(a(n-i+1,:)==1))-(n-2):n*(find(a(n-i+1,:)==1))) % 矩阵 c 的第 n-i 的第一个元素的 n-1 的字符赋值为对应于 a 矩阵中第 n-i+1 行中值为 1 的位置在 c 矩阵中的编码值
c(n-i,n)='0' % 根据之前的规则,在分支的第一个元素最后补 0
c(n-i,n+1:2*n-1)=c(n-i,1:n-1) % 矩阵 c 的第 n-i 的第二个元素的 n-1 的字符与第 n-i 行的第一个元素的前 n-1 个符号相同,因为其根节点相同
c(n-i,2*n)='1' % 根据之前的规则,在分支的第一个元素最后补 1
for j=1:i-1
c(n-i,(j+1)*n+1:(j+2)*n)=c(n-i+1,n*(find(a(n-i+1,:)==j+1)-1)+1:n*find(a(n-i+1,:)==j+1)) % 矩阵 c 中第 n-i 行第 j+1 列的值等于对应于 a 矩阵中第 n-i+1 行中值为 j+1 的前面一个元素的位置在 c 矩阵中的编码值
end
end % 完成 huffman 码字的分配
for i=1:n
h(i,1:n)=c(1,n*(find(a(1,:)==i)-1)+1:find(a(1,:)==i)*n) % 用 h 表示最后的 huffman 编码,矩阵 h 的第 i 行的元素对应于矩阵 c 的第一行的第 i 个元素
ll(i)=length(find(abs(h(i,:))~=32)) % 计算每一个 huffman 编码的长度
end
l=sum(p.*ll); % 计算平均码长
fprintf('\n huffman code:\n');
h
hh=sum(p.*(-log2(p))); % 计算信源熵
fprintf('\n the huffman effciency:\n');
t=hh/l % 计算编码效率
仿真结果如下:
please input a number:[0.30 0.25 0.20 0.15 0.10]
p =
0.3000 0.2500 0.2000 0.1500 0.1000
q =
0.1000 0.1500 0.2000 0.2500 0.3000
l =
5 4 3 2 1
a =
5 4 3 2 1
0 0 0 0 0
0 0 0 0 0
0 0 0 0 0
q =
0.2000 0.2500 0.2500 0.3000 1.0000
l =
2 1 3 4 5
a =
5 4 3 2 1
2 1 3 4 0
0 0 0 0 0
0 0 0 0 0
q =
0.2500 0.3000 0.4500 1.0000 1.0000
l =
2 3 1 4 5
a =
5 4 3 2 1
2 1 3 4 0
2 3 1 0 0
0 0 0 0 0
q =
0.4500 0.5500 1.0000 1.0000 1.0000
l =
2 1 3 4 5
a =
5 4 3 2 1
2 1 3 4 0
2 3 1 0 0
2 1 0 0 0
c =
1
0 1
c =
10
0 1
c =
10 1
0 1
c =
10 11
0 1
c =
10 11 0
0 1
c =
0
10 11 0
0 1
c =
00
10 11 0
0 1
c =
00 0
10 11 0
0 1
c =
00 01
10 11 0
0 1
c =
00 01 10
10 11 0
0 1
c =
00 01 10 11
10 11 0
0 1
c =
01
00 01 10 11
10 11 0
0 1
c =
010
00 01 10 11
10 11 0
0 1
c =
010 01
00 01 10 11
10 11 0
0 1
c =
010 011
00 01 10 11
10 11 0
0 1
c =
010 011 00
00 01 10 11
10 11 0
0 1
c =
010 011 00 10
00 01 10 11
10 11 0
0 1
c =
010 011 00 10 11
00 01 10 11
10 11 0
0 1
h =
11
10
00
011
010
ll =
2 2 2 3 3
h =
11
10
00
011
010
ll =
2 2 2 3 3
h =
11
10
00
011
010
ll =
2 2 2 3 3
h =
11
10
00
011
010
ll =
2 2 2 3 3
h =
11
10
00
011
010
ll =
2 2 2 3 3
huffman code:
h =
11
10
00
011
010
the huffman effciency:
t = 0.9903