系统响应及系统稳定性

一、实验目的

1、掌握求系统响应的方法。

2、掌握时域离散系统的时域特性。

3、分析、观察及检验系统的稳定性。

二、实验内容

1、写出系统响应及系统稳定性的Matlab程序

2、将程序在计算机上仿真实现，验证程序的正确性并完成仿真。

三、实验原理及说明

在时域中，描写系统特性的方法是差分方程和单位脉冲响应，在频域可以用系统函数描述系统特性。已知输入信号可以由差分方程、单位脉冲响应或系统函数求出系统对于该输入信号的响应，本实验仅在时域求解。在计算机上适合用递推法求差分方程的解，最简单的方法是采用MATLAB语言的工具箱函数filter函数。也可以用MATLAB语言的工具箱函数conv函数计算输入信号和系统的单位脉冲响应的线性卷积，求出系统的响应。

系统的时域特性指的是系统的线性时不变性质、因果性和稳定性。重点分析实验系统的稳定性，包括观察系统的暂态响应和稳定响应。

系统的稳定性是指对任意有界的输入信号，系统都能得到有界的系统响应。或者系统的单位脉冲响应满足绝对可和的条件。系统的稳定性由其差分方程的系数决定。

实际中检查系统是否稳定，不可能检查系统对所有有界的输入信号，输出是否都是有界输出，或者检查系统的单位脉冲响应满足绝对可和的条件。可行的方法是在系统的输入端加入单位阶跃序列，如果系统的输出趋近一个常数（包括零），就可以断定系统是稳定的[19]。系统的稳态输出是指当 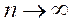    时，系统的输出。如果系统稳定，信号加入系统后，系统输出的开始一段称为暂态效应，随n的加大，幅度趋于稳定，达到稳态输出。注意在以下实验中均假设系统的初始状态为零。

四、实验设备

1、计算机

2、软件：Matlab  

五、实验方法

实例1：给定一个低通滤波器的差分方程为

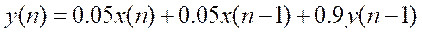
输入信号    

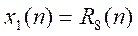
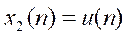
a) 分别求出系统对 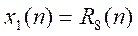    和 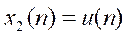    的响应序列，并画出其波形。

b) 求出系统的单位冲响应，画出其波形。

程序：

close all;

clear all;

A=[1,-0.9];

B=[0.05,0.05];

x1n=[1,1,1,1,1,1,1,1,zeros(1,40)];

x2n=ones(1,60);

hn=impz(B,A,40);

subplot(3,1,1);

stem(hn);

title('xx级xx班xx号xxx-(a)系统单位脉冲响应h(n)');

y1n=filter(B,A,x1n);

subplot(3,1,2);

stem(y1n);

title('xx级xx班xx号xxx-(b)系统对R8(n)的响应y1(n)');

y2n=filter(B,A,x2n);

subplot(3,1,3);

stem(y2n);

title('xx级xx班xx号xxx-(c)系统对u(n)的响应y2(n)');

实例2：给定系统的单位脉冲响应为

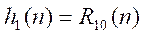
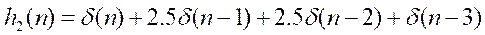
  用线性卷积法分别求 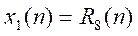    分别对系统h₁(n)和h₂(n)的输出响应，并画出波形。

程序：

close all;

clear all;

B=[0.05,0.05];

A=[1,-0.9];

hn1=[1,1,1,1,1,1,1,1,1,1,zeros(1,10)];

hn2=[1,2.5,2.5,1,zeros(1,10)];

xn1=[1,1,1,1,1,1,1,1];

yn1=conv(xn1,hn1);

yn2=conv(xn1,hn2);

subplot(2,2,1);stem(hn1);title('xx级xx班xx号xxx-响应h1(n)');

subplot(2,2,2);stem(hn2);title('xx级xx班xx号xxx-响应h2(n)');

subplot(2,2,3);stem(yn1);title('xx级xx班xx号xxx-响应y1(n)');

subplot(2,2,4);stem(yn2);title('xx级xx班xx号xxx-响应y2(n)');

六、实验结果

实例1结果：

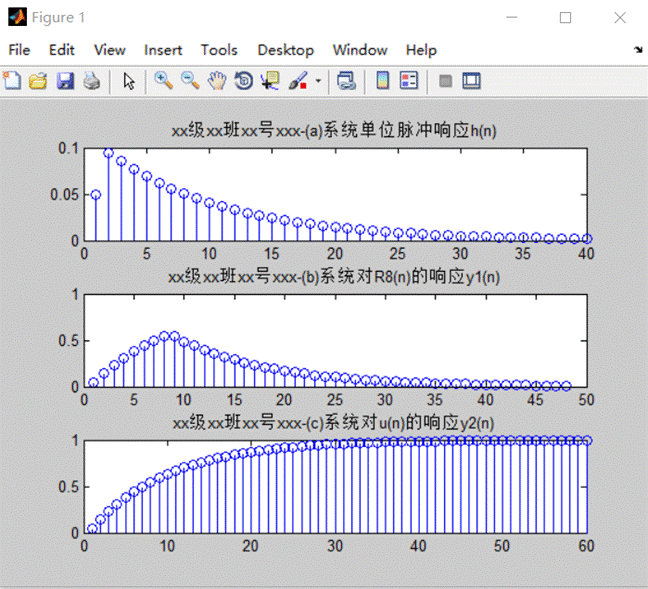
图1 实例1结果图                

实例2结果：

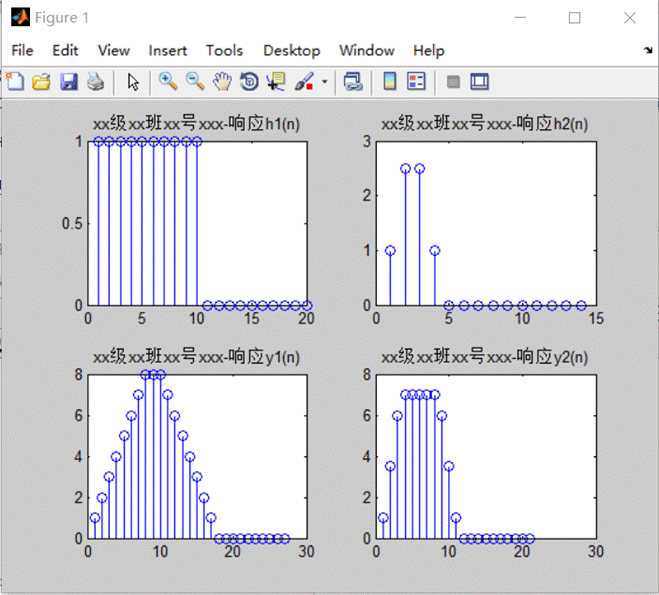
图2 实例2结果图