数字滤波器的分析与设计
一、实验目的
1、正确使用Matlab进行IIR、FIR数字滤波器的仿真、分析与设计。
2、加深理解IIR、FIR数字滤波器的特性，掌握IIR、FIR数字滤波器的设计原理与设计方法，以及IIR、FIR数字滤波器的应用。
二、实验内容
1、写出IIR、FIR数字滤波器的分析与设计的 Matlab程序
2、将程序在计算机上仿真实现，验证程序的正确性并完成仿真。
三、实验原理及说明
N阶IIR数字滤波器的系统函数为：
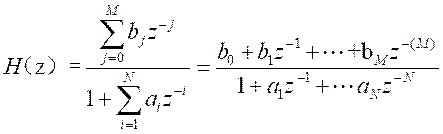
IIR数字滤波器的设计主要通过成熟的模拟滤波器设计方法来实现:将数字滤波器设计指标转换为模拟滤波器设计指标，设计出相应的模拟滤波器H(s)，再经过脉冲响应不变法或双线性变换法得到所需的IIR数字滤波器H(z)。
IIR数字滤波器设计的重要环节是模拟原型低通滤波器的设计，主要包括Butterworth、Chebyshev和椭圆等滤波器。
MATLAB信号处理工具箱中提供了IIR滤波器设计的函数。
IIR滤波器阶数选择
buttord -巴特沃斯(Butterworth)滤波器阶数选择。
cheb1ord -切比雪夫(Chebyshev)I型滤波器阶数选择。
cheb2ord -切比雪夫(Chebyshev)II型滤波器阶数选择。
ellipord -椭圆( Elliptic)滤波器阶数选择。
IIR滤波器设计
Butter -巴特沃斯(Butterworth滤波器设计
cheby1 -切比雪夫(Chebyshev)I型滤波器设计
cheby2 -切比雪夫(Chebyshev)II型滤波器设计
ellip -椭圆(Elliptic)滤波器设计
maxflat -通用的巴特沃斯(Butterworth)低通滤波器设计
yulewalk -Yule-Walker滤波器设计(直接数字滤波器设计法)
FIR滤波器
1、Butterworth滤波器设计
Butterworth滤波器是通带、阻带都单调衰减的滤波器。
(1)调用buttord函数确定巴特沃斯滤波器的阶数，格式为:
[N,Wc] =buttord(Wp,Ws,Ap,As)
输入参数: Ap,As为通带最大衰减和阻带最小衰减，以dB为单位。
Wp,Ws为归一化通带截频和阻带截频，0<Wp,Ws<1 。
输出参数: N为滤波器的阶数; Wc为截频， 0<Wc<1。
(2)调用butter函数设计出巴特沃斯滤波器，格式为:
[b,a]= butter(N, Wc,options)
输入参数: N和Wc是buttord函数返回的参数，含义见上。
Options='low', 'high', 'bandpass', 'stop',分别对应低通、高通、带通、带阻，默认情况下为低通或带通。
输出参数: b和a为设计出的FIR数字滤波器H(s)的分子多项式和分母多项式的系数矩阵。
2、Chebyshev滤波器设计
Chebyshev I型滤波器为通带纹波控制器:在通带呈现纹波特性，在阻带单调衰减。
[N,Wc] = cheb1ord(Wp,Ws,Ap,As)
[b,a]= cheby1(N,Ap,Wc,options)
参数含义与butter中参数一致。
Chebyshev II型滤波器为阻带纹波控制器:在阻带呈现纹波特性，在通带单调衰减。
[N,Wc] = cheb2ord(Wp,Ws,Ap,As)
[b,a]= cheby2(N,As,Wc,options)
参数含义与butter中参数一致。
四、实验设备
1、计算机
2、软件：Matlab
五、实验方法
实验一：设计一个数字低通滤波器，要求在0~0.2
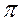(rad)内衰耗不大于3dB，在0.6 π~π(rad)内衰耗不小于60dB。
（1）若模拟低通原型采用Butterworth（巴特沃斯）滤波器:
程序：
[N,Wc]=buttord(0.2,0.6,3,60);
%调用buttord函数确定巴特沃斯滤波器的阶数[N,Wc]=buttord(WP,WS,AP,AS);
%Wp,Ws,为归一化通带截频 Ap,As通带最大衰减和阻带最小衰减
[b,a]=butter(N,Wc, 'low');
%调用butter函数设计出巴特沃斯滤波器，N为滤波器的阶数，WC为截频
freqz(b,a);
%b和a为设计出的滤波器H(S)的分子多项式和分母多项式的系数矩阵
axis([0,1,-120,0]);
grid on
title ('xx级xx班xx号xxx-巴特沃斯低通数字滤波器')
（2）若模拟高通原型采用Butterworth滤波器:
程序：
[N,Wc]=buttord(0.2,0.6,3,60);
%调用buttord函数确定巴特沃斯滤波器的阶数[N,Wc]=buttord(WP,WS,AP,AS);
%Wp,Ws,为归一化通带截频 Ap,As通带最大衰减和阻带最小衰减
[b,a]=butter(N,Wc, 'high');
%调用butter函数设计出巴特沃斯滤波器，N为滤波器的阶数，WC为截频
%b和a为设计出的滤波器H(S)的分子多项式和分母多项式的系数矩阵
freqz(b,a);
axis([0,1,-120,0]);
grid on
title ('xx级xx班xx号xxx-巴特沃斯高通数字滤波器')
（3）若模拟带通原型采用Butterworth滤波器:
程序：
Wp=[0.2 0.6];
Ws=[0.2-0.05 0.6+0.05];
Rp=3;Rs=60;
[N,Wc]=buttord(Wp,Ws,Rp,Rs);
%调用buttord函数确定巴特沃斯滤波器的阶数[N,Wc]=buttord(WP,WS,AP,AS);
%Wp,Ws,为归一化通带截频 Ap,As通带最大衰减和阻带最小衰减
[b,a]=butter(N,Wc, 'bandpass');
%调用butter函数设计出巴特沃斯滤波器，N为滤波器的阶数，WC为截频
%b和a为设计出的滤波器H(S)的分子多项式和分母多项式的系数矩阵
freqz(b,a);
axis([0,1,-120,0]);
grid on
title('xx级xx班xx号xxx-巴特沃斯带通数字滤波器')
（4）若模拟带阻原型采用Butterworth滤波器:
程序：
Wp=[0.2 0.6];
Ws=[0.2-0.1 0.6+0.1];
Rp=3;Rs=60;
[N,Wc]=buttord(Wp,Ws,Rp,Rs);
%调用buttord函数确定巴特沃斯滤波器的阶数[N,Wc]=buttord(WP,WS,AP,AS);
%Wp,Ws,为归一化通带截频 Ap,As通带最大衰减和阻带最小衰减
[b,a]=butter(N,Wc,'stop');
%调用butter函数设计出巴特沃斯滤波器，N为滤波器的阶数，WC为截频
%b和a为设计出的滤波器H(S)的分子多项式和分母多项式的系数矩阵
freqz(b,a);
axis([0,1,-120,0]);
grid on
title('xx级xx班xx号xxx-巴特沃斯带阻数字滤波器')
实验二：Chebyshev I（切比雪夫）型滤波器设计
设计一个数字带通滤波器，在100Hz~200Hz通带内纹波不大于3dB，通带两边各50Hz外是阻带，衰耗不小于40dB。抽样频率为1000Hz。
程序：
Wp=[100 200]/500;
Ws=[100-50 200+50]/500;
Rp=3; Rs=40;
[N,Wn]=cheb1ord(Wp,Ws,Rp,Rs);
%调用buttord函数确定巴特沃斯滤波器的阶数[N,Wc]=buttord(WP,WS,AP,AS);
%Wp,Ws,为归一化通带截频 Ap,As通带最大衰减和阻带最小衰减
[b,a]=cheby1(N,Rp,Wn);
%调用butter函数设计出巴特沃斯滤波器，N为滤波器的阶数，WC为截频
%b和a为设计出的滤波器H(S)的分子多项式和分母多项式的系数矩阵
freqz(b,a,512,1000);
title('Chebyshev Type I Bandpass Filter')
axis([0,500,-80,0]);
grid on
title('xx级xx班xx号xxx- Chebyshev I型滤波器设计')
实验三：设计一低通切比雪夫I型数字滤波器，通带范围0-100Hz，通带波纹3dB，阻带衰减 -30dB，系统采样率为1000Hz
程序：
taper=chebwin(35,30);
b=fir1(34,0.1,taper);
freqz(b,1,512);
title('xx级xx班xx号xxx- 低通切比雪夫I型数字滤波器')
实验四：两个频率为0.2pi和0.4pi的正弦信号叠加在一起，请用fir2函数设计一FIR滤波器将频率为0.2pi的正弦信号提取出来。
程序：
f=[0 0.8 0.8 1];
m=[1 1 0 0];
b=fir2(100,f,m);
[h,w]=freqz(b,1,128);
plot(f,m,w/pi,abs(h));
title('xx级xx班xx号xxx- FIR滤波器')
六、实验结果
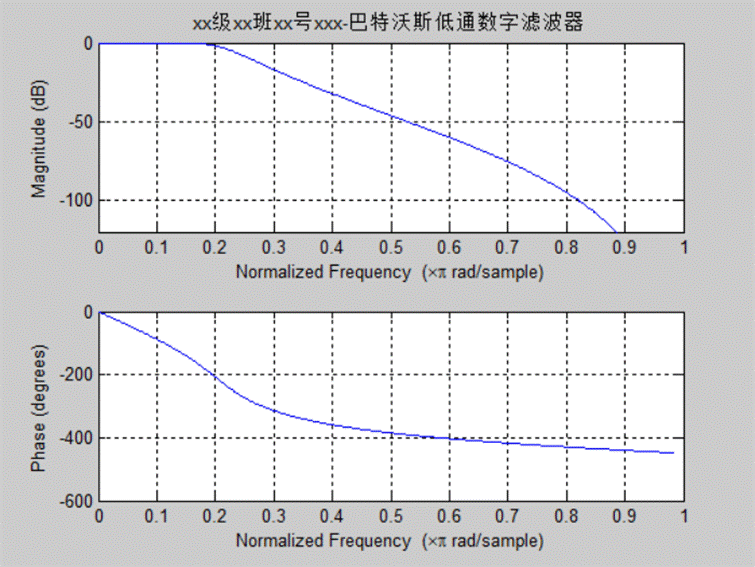
图1 巴特沃斯低通数字滤波器
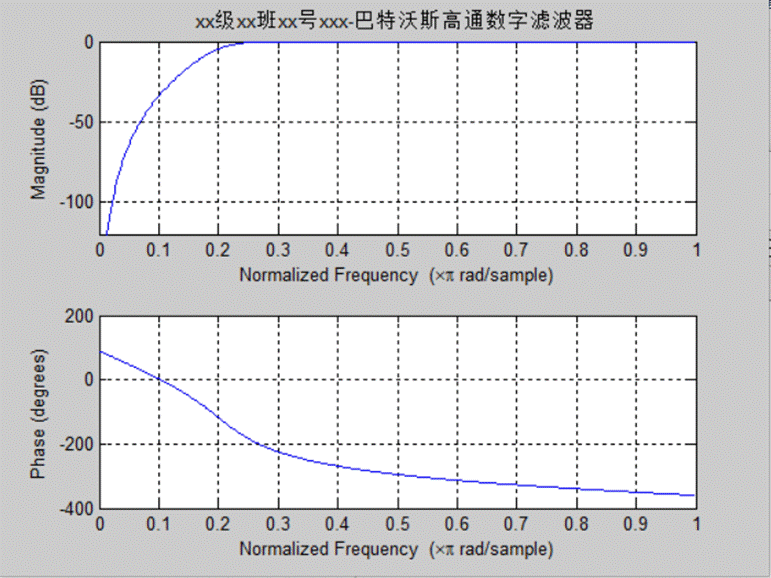
图2 巴特沃斯高通数字滤波器
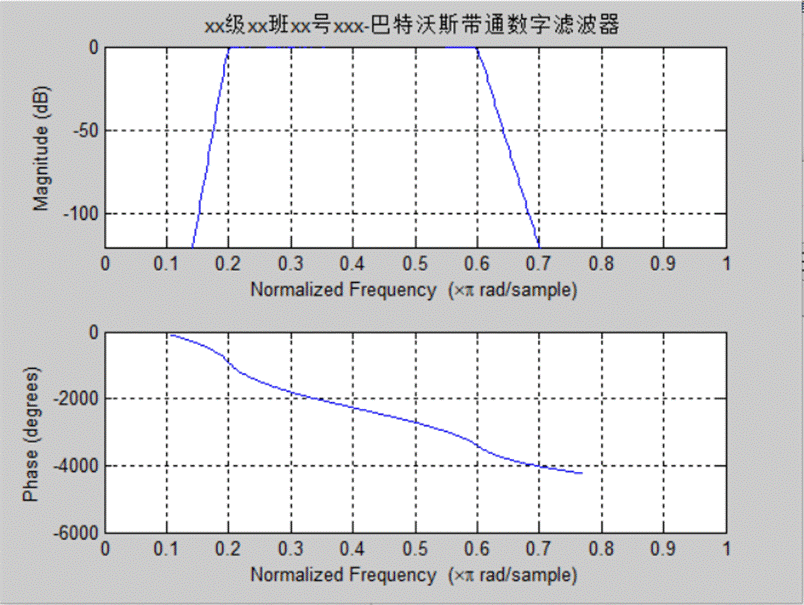
图3 巴特沃斯带通数字滤波器
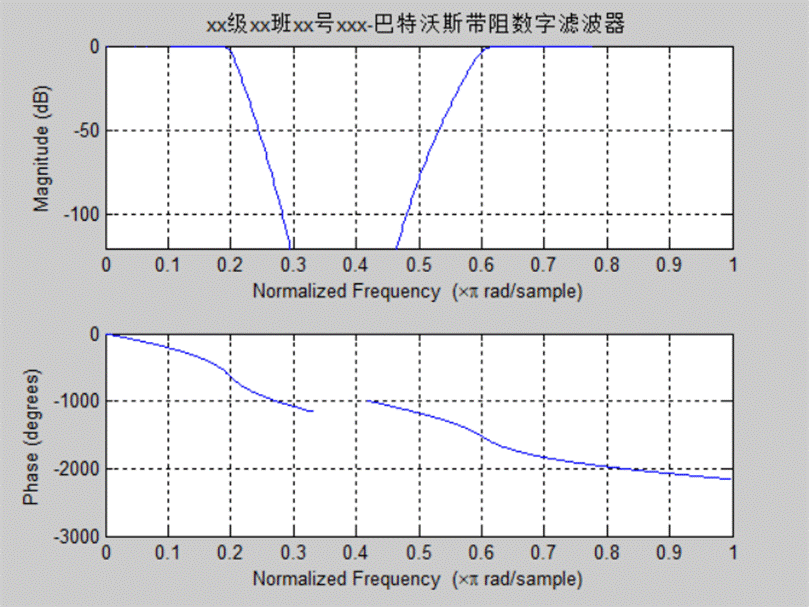
图4 巴特沃斯带阻数字滤波器
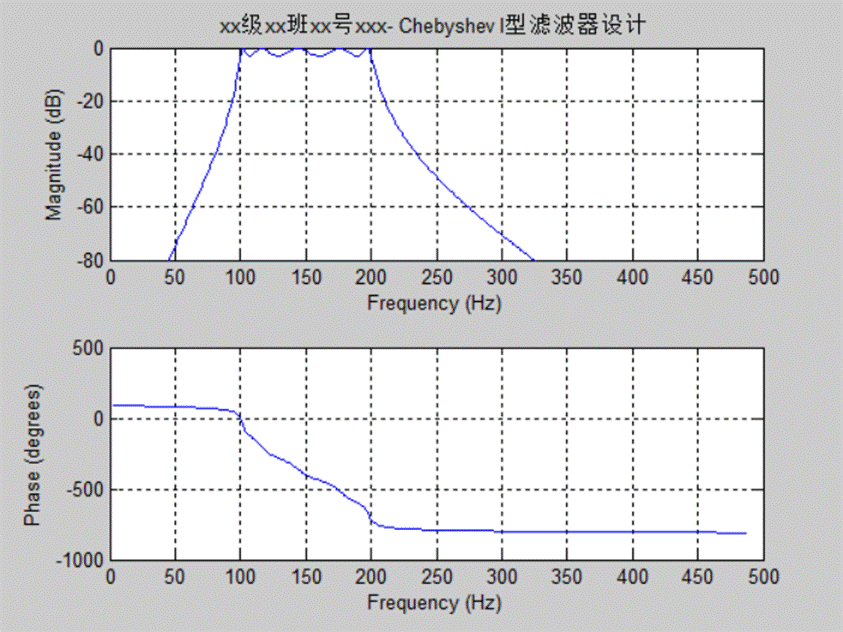
图5 ChebyshewI型滤波器设计
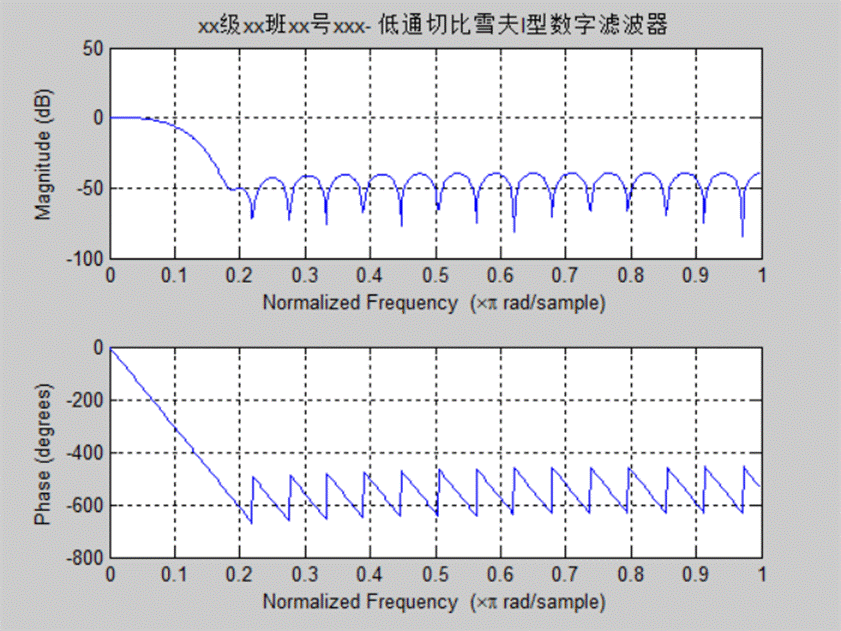
图6 低通切比雪夫I型数字滤波器
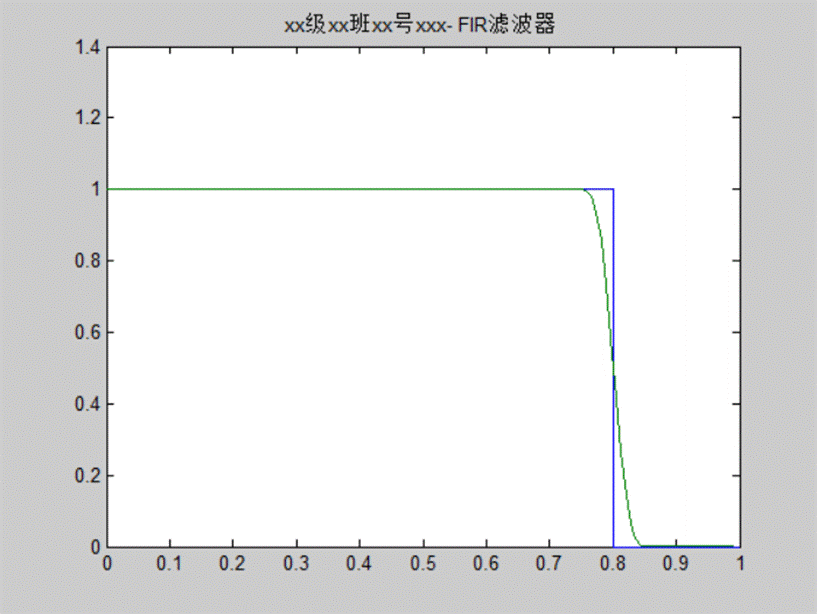
图7 FIR滤波器
