用FFT对信号作频谱分析
一、实验目的
1、掌握用FFT对信号作频谱分析的方法。
2、掌握用FFT对信号作频谱分析的特性。
3、观察分析FFT对信号的频谱。
二、实验内容
1、写出FFT对信号作频谱分析的 Matlab 程序
2、将程序在计算机上仿真实现，验证程序的正确性并完成仿真。
三、实验原理及说明
对信号进行谱分析的重要问题是频谱分辨率D和分析误差。频谱分辨率直接和FFT的变换区间N有关，因为FFT能够实现的频率分辨率是，因此要求。可以根据此式选择FFT的变换区间N。误差主要来自于用FFT作频谱分析时，得到的是离散谱，而信号（周期信号除外）是连续谱，只有当N较大时离散谱的包络才能逼近于连续谱，因此N要适当选择大一些。周期信号的频谱是离散谱，只有用整数倍周期的长度作FFT，得到的离散谱才能代表周期信号的频谱。如果不知道信号周期，可以尽量选择信号的观察时间长一些。
四、实验设备
1、计算机
2、软件：Matlab
五、实验方法
实例：对以下序列进行谱分析。
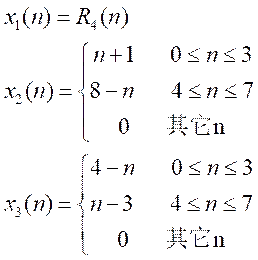
选择FFT的变换区间N为8和16 两种情况进行频谱分析。分别打印其幅频特性曲线。并进行对比、分析和讨论。
程序1：
n=0:3;
xn=[1,1,1,1];
subplot(2,2,1);
plot(n,xn,'.');
n1=0:1023;
xk1=fft(xn,1024); %快速傅里叶变换 :1024点FFT[x(n)]subplot(2,2,2);
stem(n1*2/1024,abs(xk1)); % stem画出来是离散函数，杆图
% abs(X)1.对于一般的数为，取绝对值；2.对于复数，返回复数的模
n2=0:7;
xk2=fft(xn,8);
subplot(2,2,3);
stem(2*n2/8,abs(xk2));
title('18级电信2班07号张某某-(a)8点DFT')
n3=0:15;
xk3=fft(xn,16);
subplot(2,2,4);
stem(2*n3/16,abs(xk3));
title('xx级xx班xx号xxx-(a)16点DFT')
程序2：
clear;
close all;
n=0:7;
xn=[1,2,3,4,4,3,2,1];
subplot(2,2,1);
plot(n,xn,'.');
n1=0:1023;
xk1=fft(xn,1024);
subplot(2,2,2);
stem(n1*2/1024,abs(xk1));
n2=0:7;
xk2=fft(xn,8);
subplot(2,2,3);
stem(2*n2/8,abs(xk2));
title('xx级xx班xx号xxx-(b)8点DFT')
n3=0:15;
xk3=fft(xn,16);
subplot(2,2,4);
stem(2*n3/16,abs(xk3));
title('xx级xx班xx号xxx-(b)16点DFT')
程序3：
clear;
close all;
n=0:7;
xn=[4,3,2,1,1,2,3,4];
subplot(2,2,1);
plot(n,xn,'.');
n1=0:1023;
xk1=fft(xn,1024);
subplot(2,2,2);
stem(n1*2/1024,abs(xk1));
n2=0:7;
xk2=fft(xn,8);
subplot(2,2,3);
stem(2*n2/8,abs(xk2));
title('xx级xx班xx号xxx-(c)8点DFT')
n3=0:15;
xk3=fft(xn,16);
subplot(2,2,4);
stem(2*n3/16,abs(xk3));
title('xx级xx班xx号xxx-(c)16点DFT')
六、实验结果
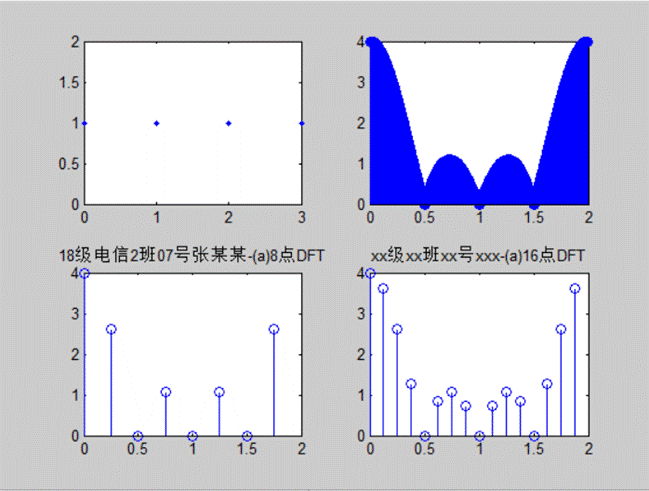
图1
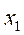(n)幅频特性曲线
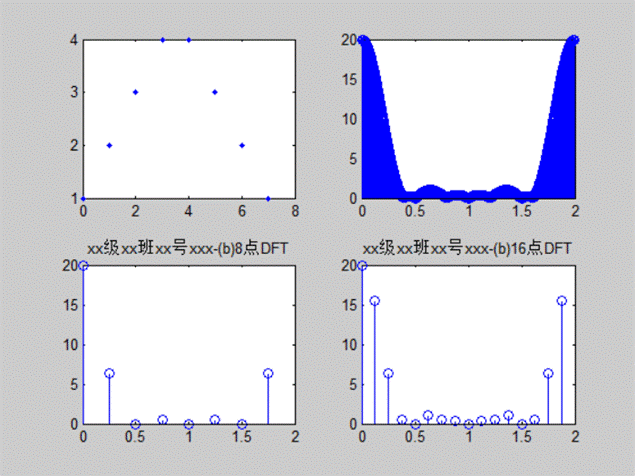
图2
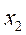(n)幅频特性曲线
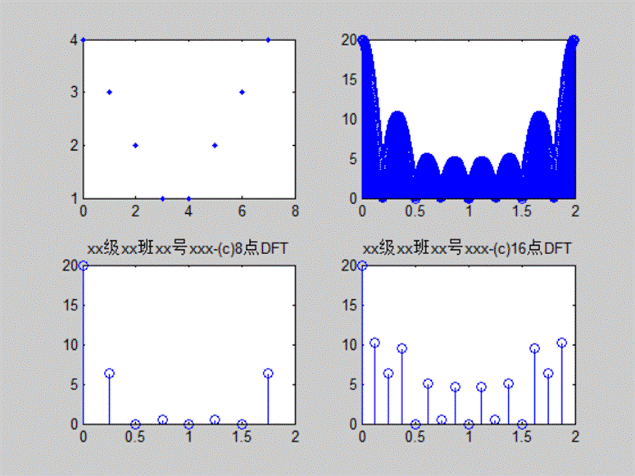
图3
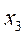(n)幅频特性曲线
