实验二 QPSK信号的误码率实验（虚拟仿真）

一、实验目的

1、掌握QPSK的误码率和误比特率原理。

2、了解QPSK的调制解调原理及方法。

二、实验内容

1、观察QPSK信号的理论和仿真的误码率和误比特率曲线波形图。

2、观察QPSK信号的星座图。

三、实验原理及说明

通信系统的抗噪声性能是指系统克服加性噪声影响的能力。在数字通信系统中，信道噪声有可能使传输码元产生错误，错误程度通常用误码率来衡量。因此，与分析数字基带系统的抗噪声性能一样，分析数字调制系统的噪声性能，也就是求系统在信道噪声干扰下的总误码率。

误码率(BER:bit error ratio)是衡量数据在规定时间内数据传输精确性的指标。误码率是指错误接收的码元数在传输总码元数中所占的比例，更确切地说，误码率是码元在传输系统中被传错的概率，即误码率=错误码元数/传输总码元数。如果有误码就有误码率。误码的产生是由于在信号传输中，衰变改变了信号的电压，致使信号在传输中遭到破坏，产生误码。噪音、交流电或闪电造成的脉冲、传输设备故障及其他因素都会导致误码（比如传送的信号是1，而接收到的是0；反之亦然）。误码率是最常用的数据通信传输质量指标。它表示数字系统传输质量的式是“在多少位数据中出现-位差错”。

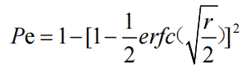  误信率，又称误比特率，是指错误接收的比特数在传输总比特数中所占的比例，即误比特率=错误比特数/传输总比特数。在数字通信系统中，可靠性用误码率和误比特率表示。

QPSK信号的误码率：

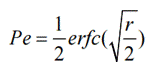
信号的误比特率：

数字调制用“星座图“来描述，星座图中定义了一种调制技术的两个基本参数：(1)信号分布；(2)与调制数字比特之间的映射关系。星座图中规定了星座点与传输比特间的对应关系，这种关系称为“映射”，一种调制技术的特性可由信号分布和映射完全定义，即可由星座图来完全定义。

首先将输入的串行二进制信息序列经串一并变换，变成m=log2M个并行数据流，每一路的数据率是R/m，R是串行输入码的数据率。IQ信号发生器将每一个m比特的字节转换成一对(pn，qn)数字，分成两路速率减半的序列，电平发生器分别产生双极性二电平信号I(t)和Q(t)，然后对coswct和sinwct进行调制，相加后即得到4PSK信号。

四、实验设备

一台安装Matlab的PC机。

五、实验方法

仿真程序：

close all;

clc;

clear all;

snr_db=(0:1:12);

sum=10000;

data=randsrc(sum,2,[0 1]);%随机取值 10000*2 矩阵中 0 和 1 值

[a1,b1]=find(data(:,1)==0&data(:,2)==0);

message(a1)=-1-1j;

[a2,b2]=find(data(:,1)==0&data(:,2)==1);

message(a2)=-1+1j;

[a3,b3]=find(data(:,1)==1&data(:,2)==0);

message(a3)=1-1j;

[a4,b4]=find(data(:,1)==1&data(:,2)==1);

message(a4)=1+1j;

scatterplot(message)

a=1;tb=1;

eb=a*a*tb;

p_signal=eb/tb;

no=eb./(10.^(snr_db/10));

p_noise=p_signal*no;

sigma=sqrt(p_noise);

for eb_no_id=1:length(sigma);

noise1=sigma(eb_no_id)*randn(1,sum);

noise2=sigma(eb_no_id)*randn(1,sum);

receive=message+noise1+noise2*1j;

resum=0; total=0;

m1=find(angle(receive)<=pi/2&angle(receive)>0); remessage(1,m1)=1+1j;

redata(m1, 1)=1; redata(m1,2)=1;

m2=find(angle(receive)>pi/2&angle(receive)<=pi); remessage(1,m2)=-1+1j;

redata(m2, 1)=0; redata(m2,2)=1;

m3=find(angle(receive)>-pi&angle(receive)<=-pi/2);

remessage(1,m3)=-1-1j;

redata(m3, 1)=0; redata(m3,2)=0;

m4=find(angle(receive)>-pi/2&angle(receive)<=0); remessage(1,m4)=1-1j;

redata(m4, 1)=1; redata(m4,2)=0;

[resum,ratiol]=symerr(data,redata); pbit(eb_no_id)=resum/(sum*2);

[total,ratio2]=symerr(message,remessage); pe(eb_no_id)=total/sum;

end

scatterplot(receive)

PE= 1-(1-1/2*erfc(sqrt(10.^(snr_db/10)/2))).^2;%理论误码率

PBIT= 1/2*erfc(sqrt(10.^(snr_db/10)/2));%理论误比特率

figure(1)

semilogy(snr_db,pe,':s',snr_db,pbit,'-*',snr_db,PE,'-o',snr_db,PBIT,':+');

legend('qpsk 仿真误码率','qpsk 仿真误比特率','qpsk 理论误码率','qpsk 理论误比特率'); xlabel('信噪比/db');

ylabel('概率 p');

仿真结果：

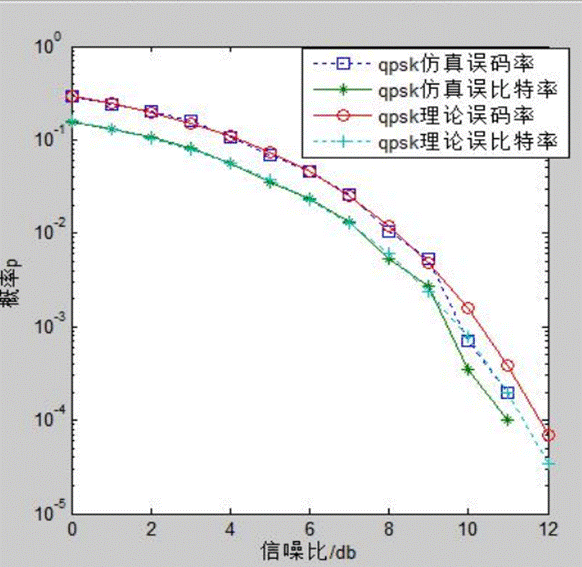
图2-1 QPSK信号的理论和仿真的误码率和误比特率曲线波形图

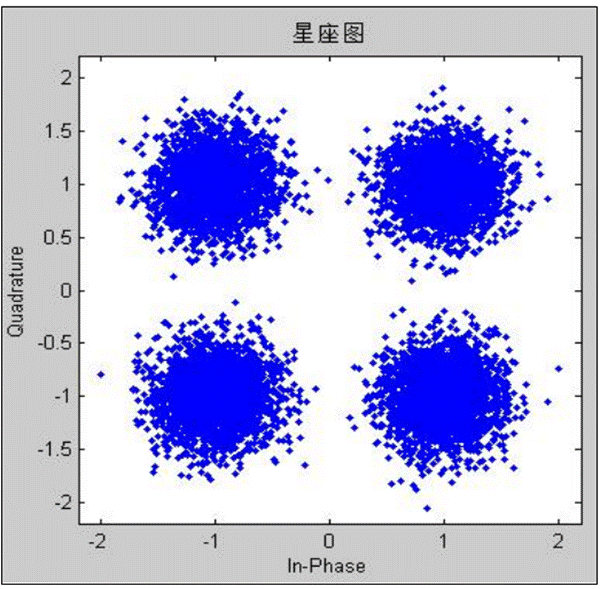
图2-2 QPSK信号的星座图