SHA编码实验

一、实验目的

了解 SHA 算法并掌握 SHA1 算法加密的应用。

二、实验目标

查看 SHA-1 加密源代码，执行程序，进行 SHA-1 加密，分析安全性。

三、实验环境

l 操作系统：Centos 7

l 其它：python 3

四、实验原理

1、SHA 算法:

安全散列算法(英语:SecureHash Algorithm)是一种能计算出一个数字消息所对应到的，长度固定的字符串(又称消息摘要)的算法。且若输入的消息不同，对应到不同字符串的机率很高;而 SHA 是 FIPS 所认证的五种安全散列算法。这些算法之所以称作“安全”是基于以下两点(根据官方标准的描述):

由消息摘要反推原输入消息，从计算理论上来说是很困难的。想要找到两组不同的消息对应到相同的消息摘要，从计算理论上来说也是很困难的。任何对输入消息的变动，都有很高的机率导致其产生的消息摘要迥异。

SHA 家族的五个算法，分别是 SHA-1、SHA-224、SHA-256、SHA-384，和 SHA-512由美国国家安全局(NSA)所设计，并由美国国家标准与技术研究院(NIST)发布;是美国的政府标准。后四者有时并称为 SHA-2。SHA-1在许多安全协议中广为使用，包括 TLS和 SSL、PGP、SSH、S/MIME 和 IPsec，曾被视为是 MD5(更早之前被广为使用的散列函数)的后继者。但 SHA-1的安全性如今被密码学家严重质疑;虽然至今尚未出现对 SHA-2有效的攻击，它的算法跟 SHA-1基本上仍然相似;因此有些人开始发展其他替代的散列算法。

SHA-1 算法流程:

1)常量:

Kt=0x5A827999(0<=t<= 19)

Kt0x6ED9EBA1(20<=t<=39)

Kt=0x8F1BBCDC(40<=t<= 59)

Kt=0xCA62C1D6(60<t< 79)

2)函数表达式:

ft(B,C,D)=(B AND C)OR(NOT B)AND D)(0 <=t<= 19)

f(B,C,D)=BXOR CXORD (20<=t<= 39)

f(B,C,D)=(B AND C)OR (B AND D)OR(C AND D)(40<t<=59)

f(B,C,D)= B XOR C XOR D(60<-t<- 79)

3)算法流程

补位

消息必须进行补位，以使其长度在对 512 取模以后的余数是 448。

补位是这样进行的:先补一个 1，然后再补 0，直到长度满足对 512 取模后余数是 448。

总而言之，补位是至少补一位，最多补 512 位(区块大小)。

补长度

补长度是将原始数据的长度补到已经进行了补位操作的消息后面。通常用一个 64 位(长度大小)的数据来表示原始消息的长度。如果消息长度不大于2^64，那么第一个字就是 0。在进行了补长度的操作以后，整个消息就变成下面这样了(16 进制格式)。

计算消息摘要

必须使用进行了补位和补长度后的消息来计算消息摘要。计算需要两个缓冲区，每个都由5个32 位(字符尺寸:32位，内部大小:160位)的字组成，还需要一个80个32位字的缓冲区。第一个5个字的缓冲区被标识为A，B，C，D，E。第一个5个字的缓冲区被标识为 HO，H1，H2，H3，H4。80 个字的缓冲区被标识为 W0，W1.….， W79。

经过一系列的计算后，最终得到的消息摘要为:

H[0]H[1]H[2]H[3]H[4]长度为 160 位(输出长度)。

五、实验过程

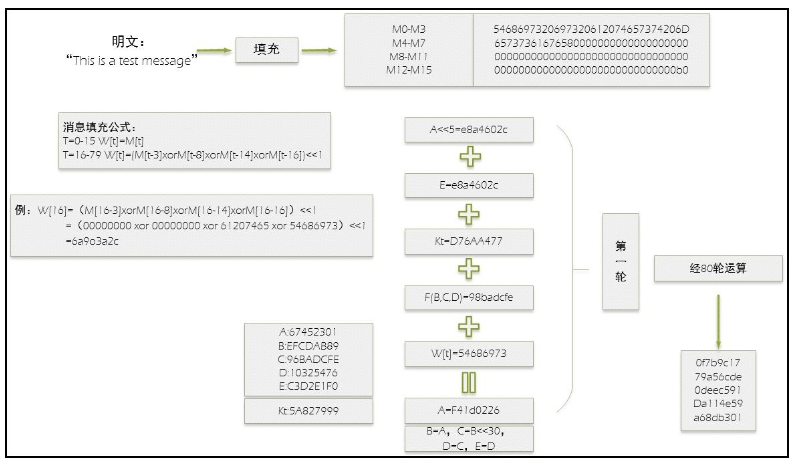
首先举一个例子了解 SHA-1 加密流程。

分别查看目录"/root/cryptography/"下的"sha-1.py"、"sha-1-2.py"、"sha-1-3.py"。这三个文件列举了三种不同的使用 python 对一段明文进行 sha-1 加密的格式。

输入命令 vim /root/cryptography/sha-1.py 査看 sha-1.py 代码内容。

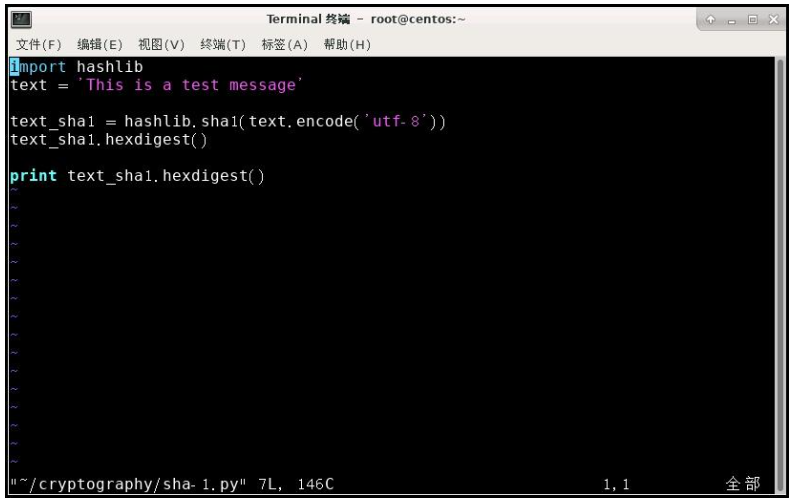
该代码先是导入了 hashlib 模块，然后需要加密的明文为“'This is a test message”，再使用 hashlib 提供的 sha1 算法对明文进行加密。最后输出加密的结果输入命令 vim /rootcryptography/sha-1-2.py 查看 sha-1-2.py 内容。

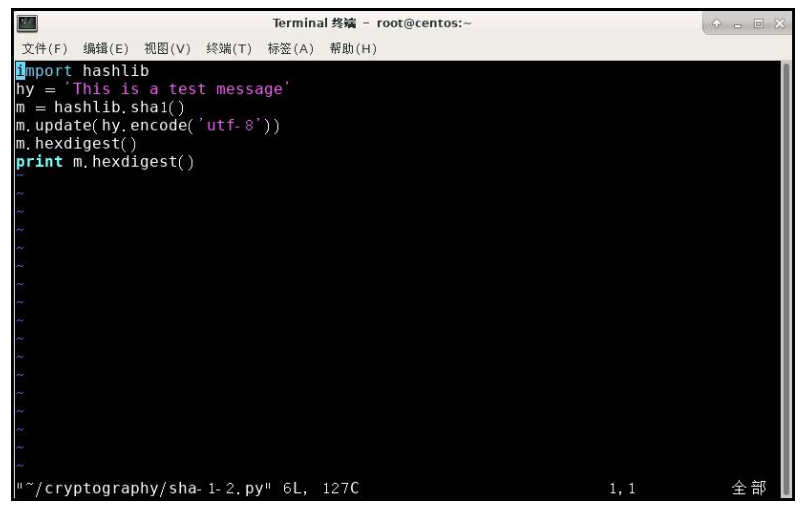
该代码与 sha1.py 相同，只是采用了不同的方式进行散列。输入命令 vimm /root/cryptography/sha-1-3.py 查看 sha-1-3.py 文件内容。

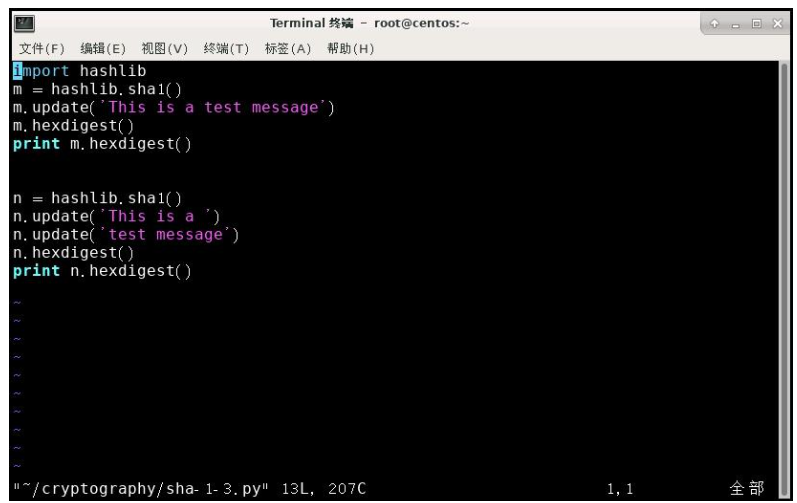
本例将明文写在了 update0)中，其中下半部分的代码将明文拆成了两部分，并分块多次调用 update0，以达到与上半部分代码相同的效果。这里需要注意:空格也是算字符的，需要注意明文是否输入正确。

输入命令 vim /root/cryptography/sha-1-4.py 查看 sha1-4 代码，该代码的作用是使用 sha1 加密方法验证文件(sha-1.py)的有效性。

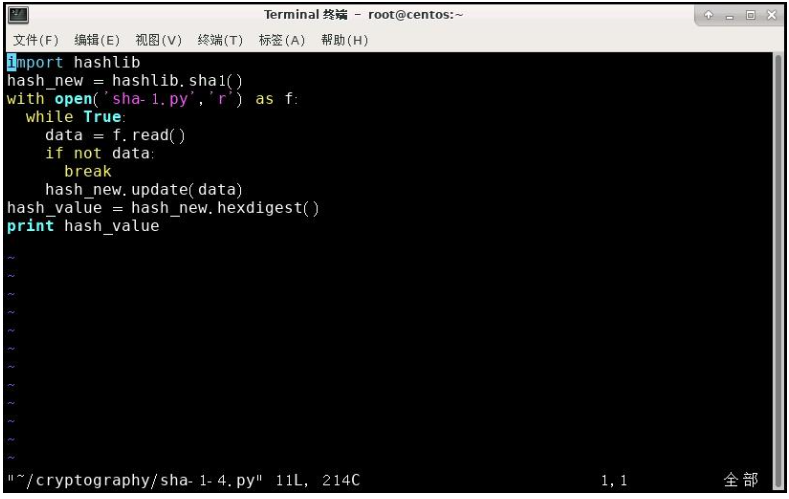
该段代码先是导入了 hashlib 模块，然后使用了其中的 sha1 算法，之后以二进制形式打开文件，并读取文件块直到读完文件，最后生成 40 位 sha1 的十六进制字符串并将其打印到屏幕

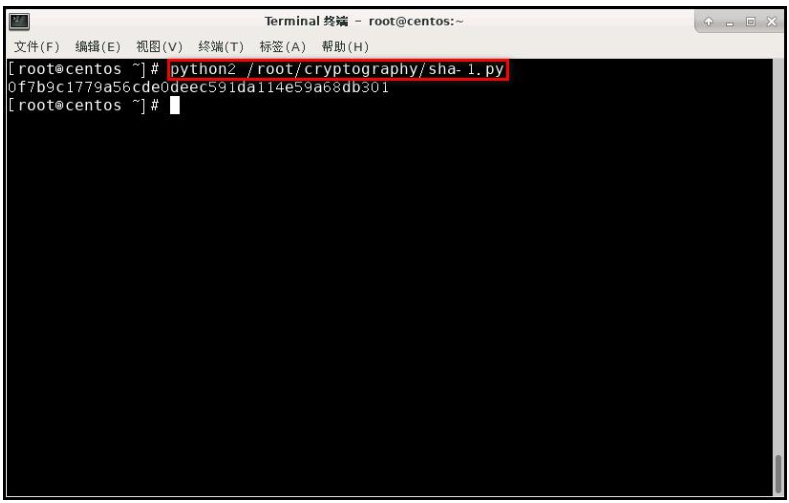
分别执行 sha-1.py、sha-1-2.py、sha-1-3.py，对明文"This is a test message"进行 shal加密。查看使用不同的代码格式得到的结果是否相同，输入命令 python2 /root/cryptography/sha-1.py 执行脚本。

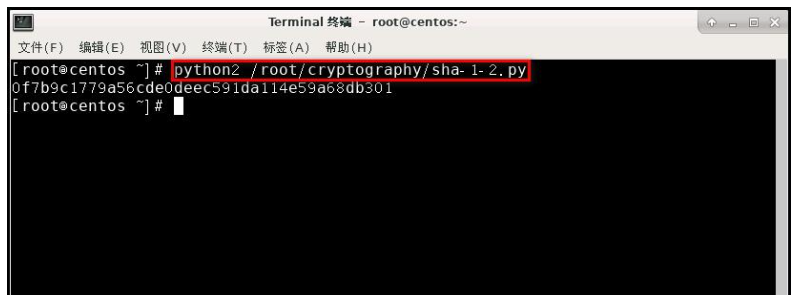
输入命令 python2 /root/cryptography/sha-1-2.py 执行脚本。

输入命令 python2 /root/cryptography/sha-1-3.py 执行脚本。

执行 sha-1-4.py，査看 sha-1.py 文件的 sha1 值。

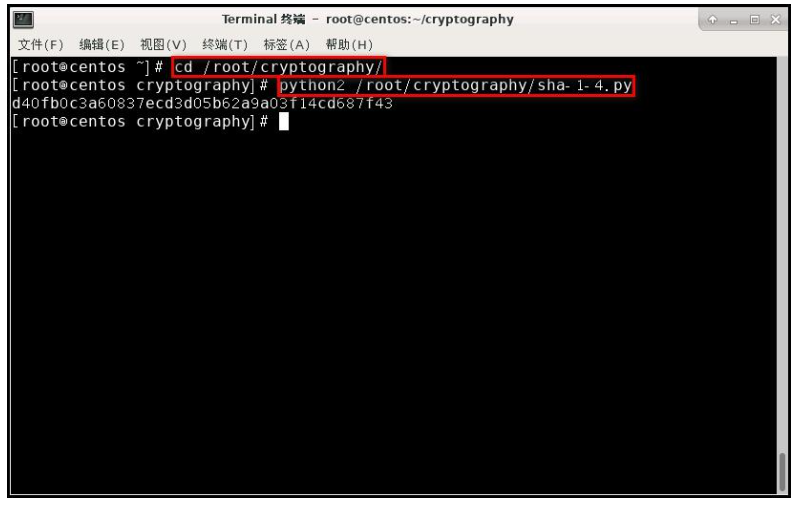
六、安全性分析

安全散列算法(Secure Hash Algorithm)能计算出一个数位讯息所对应到的，长度固定的字串(又称讯息摘要)。且若输入的讯息不同，对应到不同字串的机率很高;而 SHA 是FIPS 所认证的五种安全杂凑算法。这些算法之所以称作“安全”是基于以下两点(根据官方标准的描述):

1)由讯息摘要反推原输入讯息，从计算理论上来说是很困难的。

2)想要找到两组不同的讯息对应到相同的讯息摘要，从计算理论上来说也是很困难的。任何对输入讯息的变动，都有很高的机率导致其产生的讯息摘要迥异。

实际上，SHA-1 算法有漏洞，但也不意味着这一密码体系彻底被破解，因为破解一个密码就需要超级计算机的海量运算，而通常的安全机制中都包含多因素的防护，比如一段时间内限制密码尝试的次数等。

SHA-2 比 SHA-1 具有更高的安全性，目前还没有 SHA-2 破解的报告，但是 SHA-2 应用并不广泛，原因是在某些操作系统上缺乏支持，比如WindowsXP SP2 以前的版本。